Vers une approche transformationnelle en CAO

Horacio Vaggione

Université Paris VIII - Département de Musique

2, rue de la liberté, 93526 Saint-Denis

Résumé

En prenant parti pour une "interaction forte" entre écriture directe et traitement algorithmique, ce texte situe la CAO dans une perspective transformationnelle. Des opérations visant la complexité par la discontinuité et le feuilletage (étirements, repliements, itérations) aussi bien que par la modulation (distorsion, vectorisation) sont évoquées. Abondant dans le même sens, on propose une utilisation transformationnelle de techniques issues du champ de la modélisation et la synthèse sonore qui peuvent également élargir la palette d'outils transformationnels au niveau macroscopique.

Ecriture directe et traitement algorithmique

La problématique dont je fais état dans ce texte concerne le champ générique de la composition musicale assistée par ordinateur (CAO). A partir d'une perspective transformationnelle, elle recouvre un ensemble de techniques visant la manipulation de matériaux fortement articulés, inclus dans un réseau d'objets numériques où ils peuvent être pris comme sources, comme modulateurs, ou comme classes, fragmentés dans des sous-classes au moyen d'opérations d'extraction de saillances morphologiques qui deviennent à leur tour des nouvelles sources, des nouveaux modulateurs, et ainsi de suite.

On approche ainsi la CAO non pas comme un processus découlant d'une mise en place de formules génératives mais plutôt comme une action complexe intégrant écriture directe (ce qu'implique effectuer des choix toujours singuliers) et procédures algorithmiques transformationnelles (amplifiant ces choix en les généralisant, en les projetant sur des diverses échelles temporelles).

D'après cette approche toute intervention directe peut être considérée comme la déclaration d'un attribut particulier d'une entité quelconque; cet attribut peut dès lors être généralisé à toutes les instances successives de cette entité, et non pas rester isolé dans la localité d'une seule instance - au moins que soit ceci le cas désiré. Ainsi une action locale d'écriture a bien la possibilité de s'intégrer dans un processus algorithmique, de la même façon dont, symétriquement, le produit d'un processus algorithmique peut être transformé localement par une action d'écriture directe. De cette symétrie s'en suit une imbrication des deux possibilités d'action, sans qu'aucune ait à souffrir d'une inféodation à l'autre, pouvant au contraire amplifier mutuellement leurs implications, intégrant choix et contrainte, changement et héritage, localité et vectorisation.

On peut commencer une oeuvre en écrivant manuellement,en notation musicale ou alphanumérique,selon les situations, une collection de figures-objets auxquelles on appliquera par la suite le type de contraintes dont on désire maintenir la présence aux fins de créer de la variété contrôlée. On peut également adopter la démarche opposée, et générer des matériaux par propagation de contraintes pour les sur-qualifier après coup au moyen d'interventions directes. Cela va dépendre, en tout état de cause, de la situation musicale visée. De toutes façons -j'insiste sur ce point capital- l'image des rapports entre écriture directe et traitement algorithmique ne saurait être complète si on ignorait les possibilités d'interaction -de recursion- entre ces deux modes. Une figure écrite à la main peut ainsi, propagée dans le réseau, générer des figures en grand nombre, appartenant à la même classe. Ces figures dérivées peuvent alors être modifiées à nouveau manuellement, et on obtiendra ainsi des sous-classes en généralisant par propagation algorithmique les nouveaux attributs qu'on vient de déterminer par écriture directe. Des ensembles de figures, considérés comme des objets et appartenant à une classe, peuvent hériter des attributs d'autres classes, par modulation croisée, par convolution, par simple passation de messages entre objets. Les figures écrites à la main peuvent être pliées et repliées dans tous les sens et itérées maintes fois au moyen d'un simple objet logiciel dont on aura écrit -à la main, bien sûr- sa "partition", c'est-à-dire son code déterminant sa tâche, son mode de comportement.

Dans mon propre travail compositionnel, la production et transformation de figures musicales est basée sur des opérations de fragmentation et d'agglutination concernant des objets de toutes tailles. Souvent plusieurs niveaux temporels sont visés simultanément, ou bien travaillés séparément et plus tard mis en relation au moyen d'un autre action qui les englobe. Ainsi les figures (et les objets qui les portent) peuvent être non seulement considérées dans le sens de leurs paramètres mais aussi travaillées dans leurs "parties". Ces deux modes d'approche, que nous pouvons caractériser respectivement de paramétrique et de morphologique, sont, bien entendu, complémentaires: on peut isoler des saillances contenues dans une figure pour en créer d'autres, en les utilisant en tant que modulateurs affectés à des paramètres choisis. Je mentionnerait plus loin des techniques qui utilisent des figures en tant que "prismes modulants". Le fait d'utiliser une approche semblable tant dans des oeuvres purement électroacoustiques que mixtes ou purement instrumentales va dans le sens dont je tente dans ce texte d'en dégager quelques principes. Ainsi Tahil, pour piano seul, a été composée au moyen d'un réseau d'objets logiciels, à partir de quelques sources (objets-partitions) dont les caractéristiques morphologiques assurent un traitement conséquent de leurs parties (de leurs saillances) à partir d'une interaction (inter-modulation) généralisée. Ainsi également Kitab, pour trois instruments et dispositif audio-numérique, abonde dans la définition et l'articulation de figures, réitérées et itérées à des diverses échelles temporelles.

Etirements, repliements, vecteurs

On s'occupera dans la suite de ce texte des opérations mentionnées. Mais je dois encore aborder un aspect préalable afin de les situer dans une perspective pertinente. En effet: parler de figuration, en musique, équivaut à évoquer la problématique du thématisme. A propos de celui-ci, de son "dépassement positif" dans Erwartung et ses avatars subséquents, je renvois à l'analyse faite par Adorno dans Vers une musique informelle [Adorno 1982], analyse qui conserve, à ce qu'il me semble, un contenu d'actualité puisqu'elle traite de la problématique générale de l'articulation musicale. Je voudrais cependant ajouter que les "faits transformationnels" dont j'essaie de montrer l'enjeu relèvent d'une certaine manière de cette tendance au "dépassement positif" du thématisme. En réalité tout se passe comme si une fois accomplie au cours de ce siècle la mise à plat du thématisme traditionnel, nous avons maintenant devant nous des nouvelles perspectives à développer par rapport à la problématique posée sans cesse par le besoin d'articulation du matériau.
En tout cas le caractère banal de cette constatation ne nous épargne pas pour autant de considérer les questions complexes qu'elle pose aujourd'hui à la pensée musicale.

Si l'on se limite au stade premier, les "jeux de miroirs" classiques, également utilisés comme ossature des transformations sérielles -à savoir: rétrogradation, inversion, inversion rétrogradée- constituent des opérations strictement linéaires, où le produit est en relation de causalité directe avec la figure originale. Xenakis a signalé le fait qu'elles sont "des manipulations inconscientes des groupes finis de Klein" [Xenakis 1979, 1994]. Il a également formalisé une approche ensembliste axée sur l'organisation des hauteurs dans sa théorie des cribles [Xenakis 1963]. Cependant, les hauteurs tonales ayant de nos jours atteint la relativité que l'on connait, il s'avère intéressant d'explorer d'autres voies de transformation figurale ancrées dans un champ embrassant non seulement le combinatoire élémentaire mais aussi le topologique et l'énergétique. Ce qui nous fait évoquer la mise en place de techniques basées sur des jeux de miroirs complexes: itératifs, apériodiques, vectoriels ou non linéaires.

Nous voici donc face à un sujet très vaste dont on commence seulement à saisir l'enjeu. Il concerne des critères de formation et déformation d'entités dont le principe n'est pas sans rapport avec des opérations topologiques basées sur des étirements, repliements, reétirements, nouveaux repliements, et ainsi de suite, donnant pour résultat des morphologies très feuilletées et pleines de convolutions. Pour rester un moment en dehors de la musique: considérons par exemple la transformation du boulanger [Ekeland 1984], [Prigogine 1980], cas opératoire simple et néanmoins assez clair de génération de morphologies très feuilletées évoluant très rapidement vers l'asymétrique et le discontinu. Il existe toute une panoplie d'opérations transformationnelles issues de ce modèle topologique, opérations dans lesquelles la physique des systèmes dynamiques trouve son substrat de modélisation [Bergé 1984]. Il s'agit toujours d'opérations de feuilletage qui transforment les données initiales au moyen d'un grand nombre d'itérations. La transformation de Hénon [Hénon 1975], par exemple, basée sur l'effet combiné d'un étirement et d'un repliement, abonde dans la recherche - par des procédures itératives - d'une complexité morphologique à la fois loin de l'équilibre et fortement dirigée (vectorisée).

On pourrait multiplier les exemples concernant des opérations topologiques et vectorielles. Ils sont, il me semble, d'une grande utilité parce qu'ils éclairent des aspects importants ayant trait à la recherche d'un champ élargi de transformations figurales dans le domaine musical. Il faut cependant se garder de les voir comme des simples transferts d'opérations externes à celui-ci. Ces opérations sont en quelque sorte universelles: elles montrent une certaine manière d'approcher le fait transformationnel en général. Comme telles, elles sont immédiatement applicables à notre travail, au moyen d'algorithmes somme toute assez simples.

Mais, en abondant dans les mises en garde: il faut aussi se garder de voir dans ces transformations des simples transpositions de gestalt qu'on pourrait faire promener d'un point à un autre de l'espace euclidien sans perte aucune de leur con-figuration ou de leur identité. Les miroirs classiques visent avant tout à obtenir des transpositions; les opérations ici suggérées, comme celles dont il sera question tout de suite, visent la transformation, l'obtention d'une autre chose. J'ai insisté dans un autre travail [Vaggione 1987] sur le caractère essentiellement non-transposable des timbres, comme le montre l'échec des expériences de Ehresmann et Wessel [Erehsmann 1978], [Wessel 1979]. L'écriture traditionnelle, qui ne tient compte du phénomène du timbre que comme couleur ajoutée, qui néglige donc la corrélation des figures avec l'espace substrat spectral, est ancrée dans un espace idéalement homogène où l'on peut effectuer des transpositions sans distorsion de la structure manipulée. Je crois avoir démontré (dans le travail cité) que ceci n'était pas le cas que dans la mesure où l'on ignorait l'effet de ces transpositions sur la structure sonore (changement des centroïdes, redistribution des partiels). Je renvois donc à cette démonstration. Mais si je soulève le problème, c'est pour mieux saisir l'enjeu des opérations dont il est ici question: il s'agit de transformations, de distorsions souvent non linéaires, des vecteurs qui projettent une structure dans un espace déformant: c'est dans ceci que réside leur intérêt, et non pas dans une reformulation en d'autres termes des opérations linéaires classiques. Ces transformations acquièrent tout leur sens dès qu'on traite la musique comme l'articulation d'un flux oû surface et substrat, note et timbre, sont inextricablement liés. La musique des vingt dernières années a réalisé peu à peu les implications de sa découverte de la "composition des sons". Tout se passe dès lors comme si on ne pourrait plus séparer radicalement les opérations réalisées dans l'espace des coordonnées euclidiennes et les conséquences physiques et perceptives qui en découlent.

C'est dans ce paysage qui viennent prendre place les transformations dont on s'occupe ici. Elles s'appliquent autant aux symboles discrets de la notation musicale conventionnelle qu'aux faits sonores - qu'ils soient ou non gérés par une notation de ce type. Je rappelle que, en milieu numérique - et dans un sens strict - "tout est texte": même le son est texte, avant de passer par la conversion numérique-analogique qui "lit" le code discret du son et le transforme en fait continu. C'est pourquoi on peut par exemple produire une analyse spectrale d'une morphologie dont le résultat sera gardé sous forme de texte, pouvant par la suite être transformé en données MIDI (ou autre code macroscopique) et converti en notation musicale. La tendance, dans une approche de type CAO, est de suivre la nature de processeur de symboles qui est propre à l'ordinateur (autant qu'à la composition musicale, qui ne s'exerce que sur le discontinu -voici un point concret d'intersection entre l'outil et son application). De cela il s'ensuit une prolifération textuelle (hypertextuelle) embrassant une pluralité de niveaux emboîtés.

Cependant, ce que je propose n'est pas une simple "équi-valence" de type one-to-one entre des modalités qui, bien qu'ayant en commun le fait de leur codification discrète, relèvent néanmoins d'"ontologies régionales" différentes (que ces modalités soient, comme je l'ai dit, inextricablement liées ne signifie pas qu'elles soient en tout point semblables): il s'agit plutôt, à partir de ces conjonctions et disjonctions, d'organiser leur vectorisation commune. Bien évidement, des opérations en principe similaires appliquées à des domaines différents auront des résultats aussi caractéristiques à chaque domaine. Mais un fois le principe opératoire de leur vectorisation commune posé, nous assisterons à la mise en place de corrélations formelles évidentes.

Convolution, distorsion non linéaire

Je vais donner dans ce qui suit deux exemples techniques concernant le champ de transformations figurales. Bien entendu, ils ne constituent que deux possibilités entre toutes celles qui restent à mettre en oeuvre, voire à découvrir. Ayant employé dès 1981 des techniques telles que la convolution ou la distorsion non linéaire dans le domaine de la synthèse, j'ai songé tout naturellement à leur possible extension au domaine du macro-temps, le but étant, outre celui de disposer d'un cadre consistant de contrôle des transformations, de m'affranchir des combinatoires purement permutatives ainsi que des taux ou pourcentages de variation, qui sont souvent utilisés comme des palliatifs au manque de visée proprement figurale.

La convolution est une procédure de traitement du signal qui prend deux sons, l'un étant la source à traiter et l'autre l' "impulse" modulant. Les spectres de ces sons sont alors multipliés ensemble, et les fréquences qui sont communes aux deux sons sont amplifiées. De même, les aspects morphologiques (temporels) sont également inter-modulés. Un exemple graphique (d'après [Mont-Reynaud 1993]) peut nous faire comprendre intuitivement l'enjeu formel:

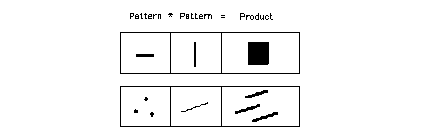
Le résultat d'une opération de convolution est donc une classe de synthèse croisée, dont les modalités sont bien connues en synthèse sonore. Appliquée au domaine macroscopique, la convolution nous permet de moduler une figure (un groupe de notes) avec une autre figure, pour obtenir soit un renforcement des notes communes, soit une soustraction de celles-ci (filtrage), soit un croisement des deux morphologies donnant naissance à d'autres figures dérivées. Cela peut affecter autant les rapports d'intervalles que de durées, ou les deux à la fois: un groupe de notes peut être traité avec des groupes de durées sans affectation d'hauteur, et on obtiendra alors des variantes rythmiques du groupe de notes. Ou, à l'inverse, des figures rythmiques peuvent être colorées par des groupes de hauteurs différents. Il faut dire que l'opération de convolution n'a pas de paramètres de contrôle autres que périphériques. Elle constitue ainsi un exemple extrême de ce qu'on pourrait appeler des techniques non-paramétriques. Tout dépend ici de la nature des morphologies mises en jeu. Ce sont les morphologies-mêmes qui déterminent les conditions initiales du processus. Bien entendu, on peut inférer des résultats à partir de ces morphologies. Ceci est montré dans l'exemple suivant:

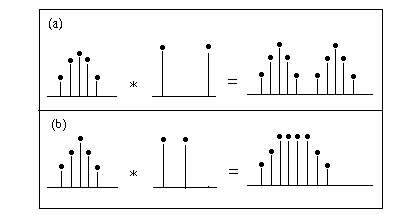
Dans (a) une figure comprenant plusieurs sons est multipliée par une autre contenant seulement deux (et qui agira comme impulse). La distance entre les deux impulses va générer un doublement de la première figure. Dans (b) la distance entre les deux impulses est plus étroite -les deux impulses se superposent à la première figure; on obtiendra alors une transformation bien spécifique de celle-ci [Roads 1993].

Des transformations de matériaux de base peuvent ainsi être multipliées formant des familles ou classes selon les attributs hérités au moyen des convolutions. Finalement, il faut s'imaginer que des opérations de convolution peuvent être effectuées sur des matériaux déjà traités, et ceci autant de fois qu'on le désire. Ainsi la convolution constitue un moyen très puissant de génération de figures de toutes tailles, reliées par des héritages d'attributs et variées par des nouveaux attributs qui s'intégreront au circuit de convolution. Programmée et "encapsulée" dans un objet, la convolution constitue l'un des objets les plus utiles d'un réseau, et cela tant au niveau du traitement du signal qu'à celui des notes.

Quant à la distorsion non linéaire (DNL), elle prend comme modèle la technique de synthèse sonore globale connue également sous l'appellation anglaise de waveshaping [Arfib 1978], [Lebrun 1979], et que j'avais utilisé auparavant comme modèle transformationnel dans le domaine du traitement du signal [Vaggione 1985]. Ici ce même modèle est détourné afin d'obtenir des transformations macroscopiques. Evidemment les conditions de ce détournement présupposent un changement radicale de domaine (d'échelle temporelle) et donc des paramètres affectés. Ce qui est transformé dans le domaine microscopique du traitement du signal est le contenu harmonique spectral, c'est-à-dire la distribution et l'évolution temporelle des partiels. Les opérations de transformation de type macroscopique (au niveau des hauteurs tonales) demandent une reformulation de l'algorithme afin de l'adapter à ce contexte. Le principe, cependant, présente un intérêt certain.

Soit donc un algorithme doté d'une fonction de transfert par laquelle on fera passer non pas une forme d'onde mais un groupe de notes, ainsi que d'un index contrôlant l'amplitude de la modulation (variable en fonction du temps). L'état de base de la fonction de transfert, celui où la figure de sortie sera équivalent en tout point à celle d'entrée, peut être représenté par un carré contenant une abscisse et une ordonnée dont les valeurs vont de -1 à +1 et sont reliés par une diagonale. La fonction laisse alors passer de façon linéaire la figure en question. Une inversion de la fonction aura comme résultat une inversion des intervalles. Mais supposons que l'on dessine, entre les deux bornes de la fonction, non pas une ligne "passe-tout" ou un filtre linéaire mais des courbes complexes, et que l'on ajoute des valeurs assez élevées de contrôle de l'amplitude de la modulation en fonction du temps: alors on obtiendra des nouvelles figures par distorsion non linéaire de la figure originale.

Ceci constitue un exemple -mais certainement pas le seul- de ce "prisme" modulant basé sur l'écriture de figures dont j'ai parlé plus haut. Il faut donc se garder de considérer l'objet DNL comme une "boîte noire". Il constitue un système où confluent trois articulations (figures-relations d'entrée, figures-fonctions modulantes, figures-enveloppes d'amplitude contrôlant les valeurs de l'index de modulation) dont on peut définir le contenu et l'intensité des interactions. Les caractéristiques des trois composantes du système ont une importance capitale dans le résultat. Cependant, une ou deux composantes ne seront pas suffisantes: on a vu qu'une simple inversion des bornes positif-négatif de la fonction de transfert nous donnerait une inversion conséquente (linéaire) de la "phase" des intervalles; on a vu aussi que les valeurs d'amplitude (index de modulation) jouent un rôle essentiel dans l'effet de distorsion produit par la fonction de transfert. Tant qu'on restera à deux composantes, l'opération de transformation correspondra au même type que celles, très linéaires, du contrepoint classique. Pour accéder à des transformations véritablement non linéaires il nous faut un "troisième corps" ou un "troisième degré de liberté" représenté par l'amplitude qui agit sur la profondeur de la modulation en fonction du temps.

En tant qu'objets logiciels inclus dans notre réseau logiciel, la convolution et la DNL nous permettront de réaliser des opérations de transformation de figures extrêmement fines concernant hauteurs, durées, ou une combinaison des deux. Tant les figures d'entrée comme de sortie, ainsi que celles de la fonction de transfert et de l'enveloppe d'amplitude de l'index de modulation, peuvent être écrites en notation musicale ou alphanumérique. Les produits des opérations sont enfin exportés vers d'autres supports, par exemple un programme de notation où l'on collecte l'ensemble des résultats, ou bien vers d'autres objets proposant d'autres fonctionnalités.

Figurations spectrales (contrôlées par des vecteurs)

Il nous faut par ailleurs prendre en compte les possibilités fournies par les éditeurs interactifs de spectres [Strawn 1987], [Rodet 1992], [Fitz 1995], lesquels permettent d'accomplir des opérations qui favorisent l'exploration des morphologies microscopiques. On peut par exemple concaténer une série de spectres sur lesquels on applique des techniques de sélection de saillances. Des spectres peuvent ainsi être travaillés dans le sens de leurs parties, par exemple en coupant / copiant / collant des "pistes" ou des "régions" afin de redistribuer la structure des partiels, ou bien pour les mélanger avec d'autres parties du même spectre ou de spectres différents. Des séries de transformations peuvent donc être réalisées dans le but de créer des successions spectrales très articulées. L'approche topologique basée sur des étirements et repliements itérés est ici applicable par manipulation directe aussi bien que par des tables/fonctions de contrôle. Cette dernière possibilitéé n'est pas à négliger, dans notre optique, parce qu'elle permet d'incorporer à ce dispositif les données issues d'un éditeur de vecteurs pouvant manipuler plusieurs paramètres physiques (vélocité, temps, accélération, position, énergie) avec lequel on pourrait définir la création et la destruction de corrélations, c'est-à-dire des champs de transformations morphologiques plus ou moins profondes émergeant en raison de l'importance du contenu d'énergie modulante.

Finalement, je voudrais citer une procédure d'analyse et d'élaboration figurale - riche de promesses - à partir de la transformation en ondelettes [Kronland-Martinet 1991]. Il m'est néanmoins impossible d'inclure ici, pour des évidentes raisons d'espace, une description de cette technique. Je vais donc me limiter à signaler la possibilité d'utiliser des ondelettes analysatrices pour l'identification et transcription non seulement de groupes de hauteurs, mais aussi de rythmes, ce qui nous donne encore une autre stratégie possible et complémentaire à ajouter à nos fins de transformation figurale. Ce travail a été déjà amorcé par plusieurs chercheurs [Kronland-Martinet 1987], [Tait 1995].

Conclusion

Je viens de décrire - en tant qu'exemples non excluants d'une approche transformationnelle de la CAO - les rudiments de quelques techniques de transformation figurale issues soit du domaine général de la topologie et de la dynamique, soit de celui du traitement du signal - ces dernières ayant été reformulées pour inclure la manipulation de données au niveau du macro-temps. Avec ceci tente de donner quelques réponses à la problématique d'une figuration musicale qui puisse tenir compte du stade actuel de la pensée compositionnelle par rapport d'une part à l'intégration du sonore dans le musical, et d'autre part par rapport aux questions posées sans cesse par le besoin d'articulation du matériau.

Bien que le passage entre différentes échelles temporelles ne soit pas toujours linéaire (cette non-linéarité étant en vérité à la racine de certains faits transformationnels) nous avons toujours la possibilité, en milieu numérique, de qualifier leurs domaines respectifs au moyen d'une vectorisation commune - la condition première qui sous-tend une telle démarche étant le fait d'une "interaction forte" entre écriture directe et traitement algorithmique.

Exemples Sonores

Références

[Adorno 1982] Th. W. Adorno, Quasi una fantasia. Trad. française de J. L. Leleu. Gallimard, Paris.

[Ames 1991] C. Ames, Introduction to 'Compose': An Editor and Interpreter for Automated Score Generation ans Score Processing. Interface 20 (2-3): 181-196.

[Amiot 1986] E. Amiot, G. Assayag, C. Malherbe, A. Riotte, Duration Structure Generation and Recognition in Musical Writing. Proceedings of the 1984 Int. Computer Music Conference. ICMA, San Francisco.

[Arfib 1978] D. Arfib, Digital Synthesis of Complex Spectra by means of Non-linear Distorted Sine Waves. Proceedings of the 1978 Int.Computer Music Conference. Northwestern University Press.

[Beauchamp 1992] J. Beauchamp et A. Horner, Extended Nonlinear Waveshaping Analysis/Synthesis Technique. Proceedings of the 1992 Int. Computer Music Conference. ICMA, San Francisco.

[Bergé 1984] P. Bergé, I. Pomeau, Ch. Vidal, L'ordre dans le chaos. Vers une approche déterministe de la turbulence. Hermann, Paris.

[Courtot 1993] F. Courtot, Entre le décomposé et l'incomposable. Les Cahiers de l'IRCAM 3: 61-88, Paris.

[Courtot 1995] F. Courtot, Vers un éditeur de figures. Deuxièmes Journées d'Informatique Musicale. LAFORIA-Institut Blaise Pascal, Paris.

[Dannenberg 1987] R. Dannenberg, CMU Toolkit Manual. Computer Science Department, Cargenie Mellon University.Pittsburg.

[Di Scipio 1991] A. Di Scipio, Caos deterministico, composizione e sintesi del suono. AIMI/DIST, Università di Gevona.

[Ekeland 1987] I. Ekeland, Le calcul, l'imprévu. Ed. du Seuil, Paris.

[Erhesman 1978] D. Erhesman et D. Wessel, Perception of timbral analogies. Rapport IRCAM n° 13, Paris.

[Fitz 1995] K. Fitz, L. Haken, B. Holloway, Lemur - A Tool for Timbre Manipulation. Proceedings of the 1995 Int. Computer Music Conference. ICMA, San Francisco.

[Gogins 1991] M. Gogins, Iterated Functions Systems Music. Computer Music Journal 15 (1): 40-48.

[Hénon 1975] M. Henon et I. Pomeau, Two Strange Atractors with a Simple Structure. Lecture Notes in Mathematics 505, p. 29.

[Herman 1993] D. Herman, Deteministic Chaos, Iterative Models, Dynamical Systems and their Application in Algorithmic Composition. Proceedings of the 1993 Int. Computer Music Conference. ICMA, San Francisco.

[Kronland-Martinet 1987] R. Kronland-Martinet, Analysis of Sound Patterns Through Wavelet Transform. Int. Journal of Pattern Recognition and Artificial Intelligence 1 (2).

[Kronland-Martinet 1991] R. Kronland-Martinet et A. Grossman, Application of Time-Frequency and Time-Scale Methods (Wavelet Transform) to the Analysis, Synthesis and Transformation of Natural Sounds. In De Poli, Piccialli et Roads (Ed.): Representations of Musical Signals. MIT Press, Cambridge, Mass.

[Kronland-Martinet 1993] R. Kronland-Martinet et Ph. Guillemain, Towards Non-linear Resynthesis of Instrumental Sounds. Proceedings of the 1993 Int.Computer Music Conference. ICMA, San Francisco.

[Lippe 1993] C. Lippe, The Ircam Signal Processing Worksation and User Group. Proceedings of the 1993 Int. Computer Music Conference. ICMA, San Francisco.

[Loy 1987] G. Loy, Player: Extensions to the C Programming Language for Parallel Processing and Music Synthesis Control. Computer Audio Research Laboratory, University of California, San Diego.

[Mathews 1969] M. Mathews, The Technology of Computer Music.. MIT Press, Cambridge, Mass.

[Mesnage 1995] M. Mesnage, Un logiciel de modélisation de partitions. Journées d'Informatique Musicale. LAFORIA, IBP, Paris.

[Moore 1985] J .A. Moore and G. Loy, CARL Startup Kit. Computer Audio Researc Laboratory, University of California, San Diego.

[Mont-Reynaud 1993] B. Mont-Reynaud, SeeMusic: A Tool for Music Visualisation.. Proceedings of the 1993 Int. Computer Music conference. ICMA, San Francisco.

[Nicolas 1987] F. Nicolas, Eloge de la complexité. Entretemps n° 3, pp. 55-67.

[Polansky 1991] L. Polansky et M. McKinney, Morphological Mutation Functions. Proceedings of the 1991 Int. Computer Music Conference. ICMA, San Francisco.

[Polansky 1992] L. Polansky, More on Morphological Mutation Functions. Recent Techniques and Developments. 1992 Int. Computer Music Conference. ICMA, San Francisco.

[Pressing 1988] J. Pressing, Nonlinear Maps as Generators of Musical Design.. Computer Music Journal 12 (2):35-46.

[Prigogine 1980] I. Prigogine, Physique, temps et devenir. Masson, Paris.

[Puckette 1990] M. Puckette, Max Manual. IRCAM, Paris.

[Riotte 1979] A. Riotte, Formalisation de structures musicales. Université Paris-VIII, Paris.

[Riotte 1989] A. Riotte, Modèles et métaphores; les formalismes en musique. In La musique et les sciences cognitives. P. Mardaga, Liège.

[Roads 1979] C. Roads, A Tutorial on Non-linear Distortion or Waveshaping Synthesis.. Computer Music Journal 3 (2): 29-34.

[Roads 1993] C. Roads, Musical Sound Transformation by Convolution. Proceedings of the 1993 Int. Computer Music Conference. ICMA, San Francisco.

[Rodet 1992] X. Rodet, Ph. Depalle, Spectral Enveloppes and inverse FFT synthesis. Proc. of AES, San Francisco.

[Scaletti 1991] C.Scaletti et K. Hebel, An Object-bassed Representation for Digital Audio Signals. In De Poli, Picialli, Roads (Eds.) Representations of Musical Signals. MIT Press, Cambridge, Mass.

[Schottstaedtt 1994] B. Schottstaedtt, CLM: Music V Meets Common Lisp. Computer Music Journal 7 (1): 11-21.

[Stockham 1969] T. Stockham, High-speed convolution and convolution with applications to digital filtering. In B. Gold et C. Rader (Eds.): Digital Processing of Signals. McGraw-Hill, New York.

[Strawn 1987] J. Strawn, Editing Time-Varying Spectra. J. Audio Eng. Soc., 35 (5): 337-352.

[Strawson 1985] P. F. Strawson, Analyse et métaphysique. Vrin, Paris.

[Tait 1995] C. Tait, Audio Analysis for Rythtmic Structure. Proceedengs of the 1995 Computer Music Conference. ICMA, San Francisco.

[Taube 1994] H. Taube, Common Music/Stella Documentation. ZKMT, Karlsruhe.

[Truax 1990] B. Truax, Chaotic Non-linear Systems and Digital Synthesis. A Exploratory Study. Proceedings of the 1990 Int. Computer Music Conference. ICMA, San Francisco.

[Vaggione 1984] H. Vaggione, The Making of Octuor. Computer Music Journal 8(2). Reprinted in C. Roads (Ed.) (1989) The Music Machine. MIT Press, Cambridge, Mass.

[Vaggione 1885] H. Vaggione, Opérations spectrales dans la composition de Thema. Rapport interne IRCAM, Paris.

[Vaggione 1987] H. Vaggione, Computerunterstütze Musikstrukturierung. Support de cours. Université Technique de Berlin.

[Vaggione 1991] H. Vaggione, A note on Object-based Composition. In O.Laske (Ed.):Composition Theory. Interface 20 (3-4): 209-216

[Vaggione 1993] H. Vaggione, Determinisme and the False Collective. About Models of Time in Early Computer-Aided Composition. Contemporary Music Review 7 (2): 91-104. Harwood Academic Publishers, Londres.

[Vaggione 1994] H. Vaggione, Timbre as Syntax: a Spectral Modeling Approach. Contemporary Music Review 11 (1): 73-83. Harwood Academic Publishers, Londres.

[Vaggione 1995] H. Vaggione, Objets, représentations, opérations. Ars Sonora Revue 2: 33-52. Paris.

[Wessel 1979] D. Wessel,Timbre Space as a Musical Control Structure. Computer Music Journal 3 (2): 45-52.

[Xenakis, 1963] I. Xenakis, Musiques Formelles. La Revue Musicale, Paris.

[Xenakis 1979] I. Xenakis, Arts, Science: Alliages. Casterman, Paris.

[Xenakis 1994] I. Xenakis, Kéleütha. L'Arche, Paris.