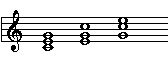
Michele Biasutti, Padova University, Via Viotti 19B, 35132 Padova, Italy. edusc01@ipdunivx.unipd.it
Abstract : The paper concerns the limits of tonal space in a task of recognition of major and minor chords. This is a report of the first tentative observations: ten subjects, amateur players of various intruments (piano, strings, trumpet), were tested in a task in which the stimuli were successions of minor and major chords centered on frequencies ranging from 39 to 8,372 Hz. The method of limits was used. Subjects were asked a binary judgment (Yes or No). Minor and major chords were presented in separate blocks.
Results show that minor and major triads lose their tonal content when placed below about 120 Hz and above about 3,000 Hz: subjects failed to recognize minor and major triads. Statistical analysis of results demonstrates a different behaviour of minor than major triads in the low range (F[2,36]=6.91; p<0.003). The loss of harmonic content for minor triads is more gradual tan for major ones.
Introduction
This paper concerns the limits of tonal space, which is defined as the limits to which we can pus tonal objects like chords, melodies and so on, at high or at low frequency ranges without making them lose their tonal (musical) content.
Schole (1934) has already pointed out that musicians can not recognize bichords at very high frequencies (approximately 8,000 Hz), and that short melodies are better reproduced than chords. A similar finding was noted by Attneave and Olson (1971). In a paper where the validity of the mel-scale was investigated, they found that subjects, for tones over 5,000 Hz, were unable to reproduce intervals made of simultaneous or consecutive tones.
Another study done by Battistelli, et al. (1988) in which the authors asked trained and untrained subjects to recognize well-known melodies in every range of frequencies, they ascertained that there is an abrupt decrease of recognition when the tonal baricentre of melodies (the mean of the frequencies constituting the melodies) shifts below a lower limit of 25 Hz and exceed an upper limit of approximately 8,000 Hz.
It is understood from this last work that melodies are recognized not only by means of their tonal content, but also because of their rhythmic pattern. In this paper we therefore decided to replicate the above mentioned results by substituting melodies with tonal objects like major and minor chords, whose tonal qualities are in a sense comparable to that of melodies. In our opinion, the previous work on single intervals or bichords could be considered either acoustic or musical, in the sense that we cannot say whether the subjects' performances involved simple acoustic discriminations or the perception of the tonal qualities.
The experiment
The experiment of the present research concerns the frequency limits in the perception of minor and major triads. In this study of minor and major triads, we use the chords on which the music of western countries is based. At this point we have a problem: there is only one chord in the same tonality per octave. If we want to have a fine discrimination about the edges of tonal (musical) space we have two possibilities: to use chords in more tonalities or to use the inversions of the chord in the same tonality. We chose to give the chord in the same tonality proceeding along frequencies by successive inversions. In this way the triads have the same tonal qualities. We used three triads per octave as one can see in Figure 1 for the major tonality: the (a) chord in root position, (b) in first inversion and (c) second inversion.
a b c
Figure 1. The major triad in root position (a), first (b) and second (c) inversion in C tonality.
Another problem was to delimitate two ranges, at low and high frequencies, which was the focus of our research. It is not helpful to explore all the range of frequencies because in the middle register, the chords are well known. We made a preliminary investigation with the aim to find the critical regions in the high and in the low register where the chords lose their tonal qualities. We utilized successions of minor and major chords centered on frequencies ranging from 16.35 Hz to 16,744 Hz. The tones employed covered a ten-octave range. The triads involved in the preliminary investigation are reported in Table 1.
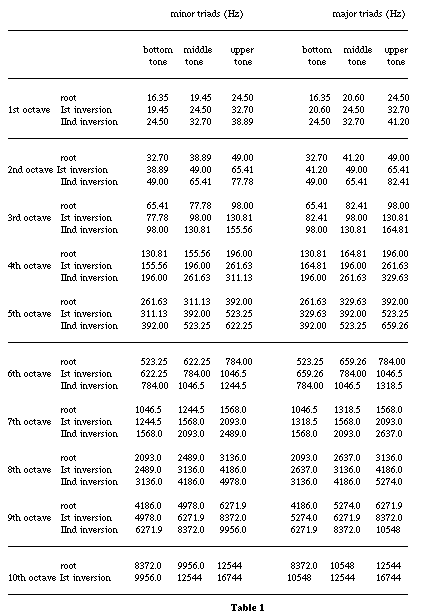
Our results found two regions: one at the low range and the other in the high range. For the experiments we utilized the second, the third, the fourth and the fifth octaves for low frequencies and the sixth, the seventh, the eighth, the nineth for high frequencies.
Method
Subjects. Ten subjects participated in the experiment. They were amateur players of various instruments (piano, strings, trumpet). Each subject was able to read music and to recognize the characteristics of minor and major chords. All subjects were able to distinguish between major and minor chords.
All listeners reported having normal hearing and none reported having absolute pitch.
Apparatus. The stimuli were generated under the control of the NeXt computer in the Computation Center of Padova University. The computer was programmed to produce the single tones of the scale context by means of a wavetek signal oscillator and the chords, by creating digital representation and playing them out through a digital to analog converter. Subjects listened to the stimuli through headphones from the computer. The stimulus levels were low enough to render aural harmonics negligible over a major portion of the range investigated.
Stimuli. The single tone of the musical chords were generated using sine-waveform. Each triad was one second long with 10 msec. amplitude rise and fall time to reduce onset and offset clicks. The interstimulus interval was 4 seconds. Chords were synthesized according to equal-tempered tuning, where each octave was divided into 12 logarithmically equal steps. The total range was from 32.70 Hz to 10,548 Hz.
The single tones of each chord were at constant loudness. The intensity of each triad follows the equal-loudness contours for pure tones presented in a free field (see Robinson & Dadson 1956).
Procedure. The method of minimal changes (method of limits) was used (see Guilford, 1954). We had two kinds of conditions for each minor and major triad: one at low frequencies and the other at high frequencies. Every condition was tested separately. Each subject listened to 48 successions of chords divided in four groups of 12 successions each: Minor low, Minor high, Major low, Major high. The succession of chords were triads in the same tonality proceeding along frequencies by successive inversions.
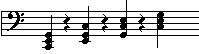 etc.
etc.
Figure 2. The major chord proceeding along frequencies by successive inversions.
You can see an example of a succession of chords in Figure 2. Subjects were asked to answer, for each sequence of triads, if it had or did not have the characteristics of a minor or a major chord.
Results
The mean distribution of subject responses are shown in Figure 3. On the abscissa are reported the mean frequencies of the three tones of each triad; the percentage of the triads recognized are reported on the ordinata. For clarity we reported only the values in the low and in the high frequency range where the triads were not well recognized.
The data obtained from the tests were applied to ANOVA. The variables were tonality (minor-major) and range (high and low). The analysis shows that there are significant differences between minor versus major triads in the low range (F [2,36]= 6.91 p<0.003) and between high and low range for major chords (F [2,36]=30.909 p<0.0005).
Discussion
To sum up, minor and major triads lose their tonal content when placed below about 120 Hz and above about 3,000 Hz: subjects fail to distinguish minor and major triads. This result agrees with the doubts of the students of this fild (see White, 1960; Deutsch, 1972; Dowling, 1973; Dowling & Hollombe, 1977; House, 1977) concerning the influence of rhythm in a task of recognizing tonal features. As to previous findings of Attneave and Olson (1971) concerning the high threshold, our results are not far from theirs. It is true that a comparison between the two works is impaired by a lack of statistical analysis in Attneave and Olson's reports, but the simple inspection of figures 1 and 4 in their report tells us that a supposed threshold may be placed between the seventh and the eighth octaves (from 4,186 Hz to 8,372), just one octave beyond our findings. We account for this difference with the less tonal content of bichords in respect of that of triads. In a sense, the higher the tonal content, the easier the loss with increasing frequencies. Nothing can be said about the low threshold, since this data is not reported in Attneave and Olson's research.
The weight of rhythmic as well as melodic division in the preservation of the tonal content in low and high ranges of acoustic space, became apparent in comparing the present findings with those of Battistelli, et al. (1988). Their melodies are recognizable below 25 Hz and beyond 8,000 Hz, respectively. We interpret the difference between our findings and theirs in the same manner as previously discussed.
Another result of interest in the present research is that there is a difference in the behaviour of triads at low and high thresholds: near the high threshold the decline in recognition is more gradual while near the lower threshold the decline is rather abrupt. We explain this fact with the different width of the critical band, that becomes wider than a tonal minor and major third in the low range (see Plomp and Levelt, 1965; Roederer, 1975; Pierce, 1983; Moore, 1977; Huron and Sellmer, 1992). Rasch and Plomp (1982, pp. 19-20) say: "If the frequencies are low, the frequency separation of thirds (and eventually also fifths) is less than a critical bandwidth so that even these intervals cause a dissonant beating. For this reason, these consonant intervals are not used in the bass register in musical compositions". On the contrary, at high frequencies the critical band is less than both thirds. It is likely that the roughness derived from the critical band would impair the recognition of triads more rapidly in the low range than in the high.
Statistical analysis of results tells us that the behaviour of minor triads is different from that of major ones at least in the lower end of tonal space (F[2,36]=6.91; p<0.003), in the sense that the loss of harmonic content is for minor triads more gradual than for major ones. We interpret this outcome in terms of low and high categorical values of chords. This finding is in accord with Biasutti and Vicario (1993).
Major triads may be a strong form which must be exactly defined in order to be recognized; minor triads may be a weak form, the definition of which could have more degrees of accuracy. In a sense, the "minor" triads can be seen as imperfect form of the "major" triads. Using to a visual analogy, there is one definition for a circle. "Compression" of the circle results in an ellipse rather than a circle. Thus, a major triad is like the circle and the minor triads, are the ellipses.
Finally some remarks about composing. Results of this experiment show that if we want have tonal meaning it is not helpfull using minor or major triads in the lower or in the upper register. This not means that we can not use chords in those ranges: we can use chords with other meanings. Contemporary and computer music showed the use of a lot of new principles in composition. We can use chords at the edge of tonal space to create illusions or other new meanings.
These data are the first results of a series of experiments consisting in studing the relationship between major and minor triads.
Figure 3. The mean distributions of subject responses.
References
Attneave, F., Olson, R. (1971). Pitch as medium: A new approach to psychophysical scaling. American Journal of Psychology, 84, 147-166.
Battistelli, A., Odoardi, C., Vicario G. B. (1988). Riconoscimento di melodie ai limiti dello spazio tonale. Giornale italiano di Psicologia, 15 (2), 235-248.
Biasutti, M., Vicario, G. B. (1993). Prestazioni di soggetti competenti e non competenti in un compito di valutazione di accordi musicali. Giornale italiano di Psicologia, 20 (3), 453-473.
Deutsch, D. (1972). Octave generalization and tune recognition. Perception & Psychophysics, 9, 348-349.
Dowling, W. J. (1973). Rhythmic groups and subjective chunks in memory for melodies. Perception & Psychophysics, 14, 37-40.
Dowling, W. J., Hallombe, A. W. (1977). The perception of melodies distorted by splitting into several octaves. Perception & Psychophysics, 21, 60-64.
Guilford J. P. (1954). Psychometric Methods. New York: McGraw-Hill.
House, W. J. (1977). Octave generalization and identification of distorted melodies. Perception & Psychophysics, 21, 586-589.
Huron, D., Sellmer, P. (1992). Critical Bands and the spelling of Vertical Sonorities. Music Perception, 10 (2), 129-150.
Moore, B. C. (1977). Introduction to the Pshychology of Hearing. London: MacMillan Press.
Pierce J. R. (1983). The science of musical sound. New York: Scientific American Books, Inc.
Plomp, R., Levelt, W. J. M. (1965). Tonal consonance and critical bandwidth. Journal of the Acoustical Society of America, 38, 548-560.
Rasch, R. A., Plomp, R. (1982). The perception of musical tone. In D. Deutsch (Ed.), The psychology of music (pp. 1-24). New York: Academic Press.
Robinson, D. W. & Dadson R. S. (1956). A re-determination of equal-loudness relations for pure tones. British Journal of Applied Physics, 7.
Roederer, J. G. (1975). Introduction to the phisics and psychophysics of music. New York: Springer-Verlag.
Schole, H. (1934). Experimentelle Untersuchungen an höchsten und kürzensten Tönen. Zeitschrift für Psychologie, 131, 1-65.
White, B. W. (1960). Recognition of distorted melodies. The American Journal of Pshychology, 73, 100-107.